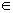[0,1], N=5, M=10, a=1(1)10, b=1(1)5.Цель курса: подготовка специалиста-математика к эффективному использованию современных методов восстановления сеточных функций, использования нерегулярных сеток для решения нестационарных краевых задач.
Задачи учебного курса:
Изучение основных понятий теории сплайнов. Получение основных навыков исследования и применения сплайновых методов к решению прикладных задач, формирование представлений о содержании, тенденциях развития, а также роли этой теории в создании новых вычислительных алгоритмов.
Место курса: входит в блок специальных дисциплин, дает основы фундаментальных знаний в области теории восстановления сеточных функций, математического моделирования прикладных задач в областях сложной формы.
Требования к уровню освоения курса: студент должен овладеть системой знаний о теоретических основах сплайнов, уметь применять эти функции к решению прикладных задач.
Введение в предмет. (4 ч)
Интерполяция сплайнами одной переменной. Полиномиальная интерполяция Лагранжа и ее сходимость. Интерполяционный сплайн первой степени. Построение кубического сплайна через моменты. Построение кубического сплайна через наклоны. Параболические сплайны. Метод прогонки для систем с трехдиагональными матрицами. Параметрические сплайны. Кубические нелокальные сплайны. (10 ч)
Представление сплайнов через В-функции. Свойства В-сплайнов. Построение интерполяционного кубического сплайна. (6 ч)
Сплайны двух переменных. Билинейные сплайны. Локальные сплайны первой степени на нерегулярной сетке. (8 ч)
Применение кубических сплайнов для решения краевых задач. Метод сплайн-коллокации. Итерационно-интерполяционный метод. Разностные схемы итерационно-интерполяционного метода. Экономичные схемы сплайновой интерполяции. (6 ч)
Стечкин С.Б., Субботин Ю.Н. Сплайны в вычислительной математике. -М.: Наука, 1976. —248 с.
Завьялов Ю.С., Леус В.А., Скороспелов В.А. Сплайны в инженерной геометрии. -М.: Машиностроение, 1985. - 224 с.
Марчук Г.И. Методы вычислительной математики. - М.: Наука 1980.- 536 с.
Завьялов Ю.С., Квасов Б.И., Мирошниченко В. Методы сплайн-функций. - М.: Наука, 1980. - 352 с.
Де Бер К. Практическое руководство по сплайнам. - М.; Радио и связь, 1985. - 304 с.
Алберг Дж., Нильсон Э. Уолв Дж. Теория сплайнов и ее приложения. - М.: Мир, 1972. –ЗI6с.
Шенен П., Коснар М., Гардан И. и др. Математика и САПР Кн. -М.: Мир, 1988. -204 с.
Берцун В.Н. Кубические сплайны. Томск. ТГУ 1989. -15 с.
Бердышев В.К, Субботин Ю.Н. Численные методы приближения функций. - С. 1979. -120с.
Верш К, Завьялов Ю.С., Павлов Н.Н. Экстремальные свойства сплайнов и задача сглаживания. -Н. 1988. -101 с.
Носач К.В. Решение задач аппроксимации с помощью персональных компьютеров. -М.: МИКАП, 1994. —382 с.
Руса С.В. Разностные сплайн-схемы для задач тепло- и массопереноса. Иркутск, 1990.
Буйнис К.А. Латвийский матем. ежегодник. Вып. 29, Рига, 1985. -с. 194-197.
Потапова Н.А., Русанов С.В. Построение неравномерных разностных схем с помощью кубических сплайнов. МГУ, вып. 6, 1981. -с. 22-30.
Фокс А., Пратт М. Вычислительная геометрия: Применения в проектировании и на производстве. М.: Мир, 1922. -304 с.
Русанов С.В. Методы сплайн-функций в вычислительной гидродинамике. Пермь, 1987.-88 с.
Абалакин И. В., Жохова А.К, Четверушкин Б.Н. Кинетически согласованные разностные схемы на нерегулярных сетках. Сб. Математическое моделирование. 1977. Т. 9.*7.-с. 44-53.
Каханер Д., Маулер К., Юзн С. Численные методы и программное обеспечение. М.: Мир, 1998. -575 с.
Гришин А.М., Берцун ВН., Зинченко В.И. Итерационно-интерполяционный метод и его приложения. Томск, 1981. - 160 с.
Берцун В.Н. Интерполяция В-сплайнами. Томск, 1996. - 9 с.
Задачи для самостоятельной работы.
Задание №1. Построить кубический сплайн S(x) через моменты или наклоны для одной из функций табл.1, заданных на сетке ω для N=5,10. Оценить погрешность интерполяции в центрах интервалов сетки v .
|
Функция |
Интервал |
Тип дополнит. условия |
|
exp(x) |
[0; 2] |
I |
|
exp(-x) |
[-1; 1] |
II |
|
1/(1+25x2) |
[-1; 1] |
I |
|
sin(x) |
[0; 2π] |
III |
|
ln(x) |
[0,9; 1,9] |
I |
|
|x| |
[-1; 1] |
I |
|
tg(x) |
[0; π/4] |
IV |
|
cos(x) |
[0; π/4] |
II |
|
ln(x)2 |
[0,9; 1,9] |
I |
|
sin(5x) |
[0; 1] |
II |
|
(1-x)/(1+x) |
[0; 1] |
I |
Задание №2. Для функций из задания №1 построить сплайн через В–функции.
Задание №3. Построить билинейный и бикубический сплайны для
функций f(x,y)=exp(axy),
f(x,y)=sin(bxy), (x,y)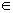[0,1], N=5, M=10, a=1(1)10, b=1(1)5.
Задание №4. Методом сплайн – коллокации найти приближенное аналитическое решение стационарной краевой задачи.
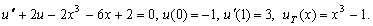
Сравнить полученное решение с точным.
История возникновения сплайновой интерполяции.
Преимущества и недостатки лагранжевой и сплайновой интерполяции.
Построение кубического сплайна через моменты.
Построение кубического сплайна через наклоны.
Параболические сплайны.
Параметрические сплайны
Свойства В-сплайнов.
Построение интерполяционного кубического сплайна через В- функции.
Метод циклической прогонки.
Сглаживающие сплайны, сглаживание сеточных функций.
Билинейные сплайны.
Триангуляция Делоне. Локальные сплайны первой степени на нерегулярной сетке.
Бикубические сплайны.
Сглаживающая кривая Безье и составные В – сплайновые кривые.
Итерационно – интерполяционный метод решения краевых задач.
Разностные схемы сплайновой интерполяции.
Экономичные схемы сплайновой интерполяции для решения двумерных нестационарных краевых задач.
Параллельные алгоритмы для построения билинейных сплайнов.
Общий объем самостоятельного освоения ресурса100 часов. Из них с использованием компьютера – 34 ч.
Требования к уровню освоения курса: студент должен овладеть системой знаний о теоретических основах сплайнов, уметь применять эти функции к решению прикладных задач.