Введение
В различных алгоритмах вычислительной математики часто возникает необходимость
решения следующих задач: приближенного восстановления таблично заданной
функции, приближенного представления функций, сглаживания функций,
приближенного вычисления по функции функционалов и операторов, приближенного
решения функциональных уравнений, описания форм сложных изделий и их
изображения с помощью компьютерной графики.
Если на сетке 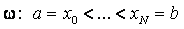 заданы значения некоторой сеточной функции
заданы значения некоторой сеточной функции
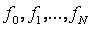 ,
то интерполяционный многочлен Лагранжа для
,
то интерполяционный многочлен Лагранжа для
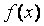 решает задачу интерполирования на
решает задачу интерполирования на 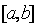 .
Однако практическое применение таких многочленов при больших
.
Однако практическое применение таких многочленов при больших
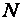 для функций с особенностями и малой гладкостью ограничено.
Этот недостаток можно устранить, если использовать полиномиальные
сплайны (spline – упругий стержень, рейка). Полиномиальным сплайном
называют определенную в области
для функций с особенностями и малой гладкостью ограничено.
Этот недостаток можно устранить, если использовать полиномиальные
сплайны (spline – упругий стержень, рейка). Полиномиальным сплайном
называют определенную в области
 кусочно-полиномиальную функцию
кусочно-полиномиальную функцию 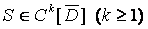 такую, что ее сужение на
такую, что ее сужение на 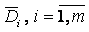 ,
является многочленом [1, 2].
,
является многочленом [1, 2].
Простейшим примером полиномиального сплайна первой
степени является ломаная, «склеенная» во внутренних узлах сетки ω из
линейных функций. Наиболее употребительными в приложениях стали кубические
сплайны, которые на каждом интервале сетки ω являются многочленами третьей степени. Впервые такие
сплайн-функции рассматривались Шенбергом (1946). Важную роль в развитии теории
сплайнов сыграло обнаруженное Холлидеем (1957) экстремальное свойство
интерполяционных кубических сплайнов. Базисные функции с локальным носителем (В
– сплайны) позволяют записать сплайн в виде линейной комбинации базисных
функций.
Использование сплайн-функций для приближенного решения краевых задач
способствовало развитию метода конечных элементов, получению разностных схем
сплайновой интерполяции. Вейвлет – анализ (wavelet–маленькая волна), возникший в конце
прошлого века, активно начинает использоваться для решения нестационарных
задач сжатия и обработки изображений. Сплайн – вейвлеты, являющиеся составной
частью этой теории, основаны на использовании В – сплайнов.
Сплайновые методы успешно применяются при решении двумерных задач
интерполяции и сглаживания функций. Этот подход оказывает свое плодотворное
влияние и на создание параллельных вычислительных алгоритмов суперкомпьютерной
математики для решения сложных задач науки и техники.
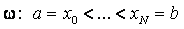 заданы значения некоторой сеточной функции
заданы значения некоторой сеточной функции
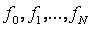 ,
то интерполяционный многочлен Лагранжа для
,
то интерполяционный многочлен Лагранжа для
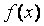 решает задачу интерполирования на
решает задачу интерполирования на 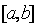 .
Однако практическое применение таких многочленов при больших
.
Однако практическое применение таких многочленов при больших
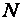 для функций с особенностями и малой гладкостью ограничено.
Этот недостаток можно устранить, если использовать полиномиальные
сплайны (spline – упругий стержень, рейка). Полиномиальным сплайном
называют определенную в области
для функций с особенностями и малой гладкостью ограничено.
Этот недостаток можно устранить, если использовать полиномиальные
сплайны (spline – упругий стержень, рейка). Полиномиальным сплайном
называют определенную в области
 кусочно-полиномиальную функцию
кусочно-полиномиальную функцию 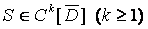 такую, что ее сужение на
такую, что ее сужение на 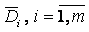 ,
является многочленом [1, 2].
,
является многочленом [1, 2].