
1-ой аксиоме счетности
Топологическое пространство удовлетворяет 1-ой аксиоме счетности, если каждая точка имеет счетную фундаментальную систему окрестностей.
2-ой аксиоме счетности
Топологическое пространство удовлетворяет 2-ой аксиоме счетности, если оно имеет счетную базу топологии.
Аксиомами отделимости
Это так называемые аксиомы: Аксиома T0, Аксиома T1, Аксиома T2 = Аксиоме Хаусдорфа, Аксиома T3, Аксиома T4, Аксиома регулярности, Аксиома нормальности.
Аксиома T0
Для любых различных точек в топологическом пространстве по крайней мере у одной из них существует окрестность, не содержащая другую точку.
Аксиома T1
Для любых двух различных точек в топологическом пространстве у каждой из них существует окрестность, не содержащая другую точку.
Аксиома T2
(часто также называемая аксиомой Хаусдорфа): любые две различные точки имеют непересекающиеся окрестности.
Аксиома T3
= Аксиома регулярности + Аксиома T1
Аксиома T4
= Аксиома нормальности + Аксиома T1
Аксиома нормальности
Любые два замкнутых непересекающихся множества имеют непересекающиеся окрестности.
Аксиома регулярности
Любое замкнутое множество и не принадлежащая этому множеству точка имеют непересекающиеся окрестности.
Александров Павел Сергеевич (1896-1982)
Основные труды по топологии и теории функций действительного переменного, в этих областях получил ряд выдающихся результатов. П.С.Александров создал современную топологическую школу, получившую мировое признание. Автор сотен монографий, учебников и учебных пособий.
Топология, состоящая всего из двух множеств: 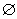 и X , называется тривиальной или антидискретной топологией.
и X , называется тривиальной или антидискретной топологией.
База топологии
Семейство 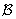 открытых множеств называется базой топологии, если любое открытое множество можно представить в виде объединения некоторого объединения элементов из
открытых множеств называется базой топологии, если любое открытое множество можно представить в виде объединения некоторого объединения элементов из 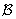 .
.
Бутылка Клейна
Фактор-пространство, полученное из прямоугольника и имеющее следующую развертку.
Вейль Герман Клаус Хуго (1885-1955)
Немецкий математик и физик. Окончил Геттингенский университет. Работал в различных областях математики. Первые работы посвящены тригонометрическим рядам, рядам по ортогональным функциям и почти периодическим функциям. Наиболее значителен комплекс работ Вейля по теории непрерывных групп и их представлений с применениями к проблемам геометрии и физики. В области философии математики Вейль известен как представитель интуиционизма.
Внутренность
Множество всех внутренних точек множества A называется его внутренностью и обозначается 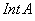 .
.
Внутренняя точка
Точка 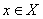 называется внутренней точкой множества A , если у нее существует окрестность Ox такая, что
называется внутренней точкой множества A , если у нее существует окрестность Ox такая, что 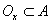 .
.
Всюду плотное множество
Множество A называется всюду плотным в топологическом пространстве X , если его замыкание 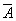 равно X .
равно X .
Выделения ручки
Процедура, описанная в леммах 33-35.
Выделения пленки Мебиуса
Процедура, описанная в леммах 37 и 38.
Выдающийся немецкий математик. Окончил Кенигсбергский университет. Исследования Гильберта оказали большое влияние на развитие многих разделов математики, а его деятельность в Геттингенском университете в значительной мере содействовала тому, что Геттинген в 1-й трети XX в. был одним из основных мировых центров математической мысли.
Гомеоморфизм
Отображение 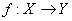 называется гомеоморфизмом, если выполнены следующие три условия:
называется гомеоморфизмом, если выполнены следующие три условия:
1) f есть биекция X на Y ;
2) f непрерывно;
3) f -1 непрерывно.
Гомеоморфные пространства
Если между топологическими пространствами существует гомеоморфизм, то они называются гомеоморфными пространствами.
Граничная точка
Точка x называется граничной точкой множества A , если любая ее окрестность Ox имеет непустое пересечение как с множеством A, так и с его дополнением X \ A .
Двусторонняя поверхность
Двумерное связное многообразие, которое можно раскрасить двумя разными цветами.
Граница
Множество всех граничных точек множества A называется его границей и обозначается FrA .
Дискретная топология
Дискретной топологией называется семейство всех подмножеств данного множества.
Дискретным топологическим пространством
Множество, наделенное дискретной топологией, называется дискретным топологическим пространством.
Замкнутые множества
Подмножество F называется замкнутым, если его дополнение X \ F является открытым.
Замыкание
Множество всех точек прикосновения множества A называется замыканием множества A и обозначается символом 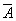 .
.
Изолированная точка
Точка x множества A называется его изолированной точкой, если она имеет окрестность Ox такую, что 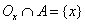 .
.
Индуцированная топология
Пусть A есть подмножество в топологическом пространстве 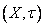 . Семейство
. Семейство 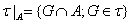 называется индуцированной топологией.
называется индуцированной топологией.
Немецкий математик. Родился в Петербурге. В 1867 г. окончил Берлинский университет. Является создателем теории множеств и начал абстрактной топологии. В 1897 г. отошел от научного творчества.
Крендель
Поверхность, полученная в результате склейки двух торов, в которых вырезаны две круглые дырки с отождествлением краев этих дыр.
Компактность
Топологическое пространство называется компактным, если из любого его открытого покрытия можно извлечь конечное подпокрытие.
Куратовский Казимеж (1896-1980)
Польский математик. Работал в области топологии, теории множеств и теории функций. Был директором Математического института Польской АН
Лемма Цорна
Это утверждение эквивалентно аксиоме выбора в абстрактных теориях множеств. Потому и само оно должно восприниматься как независимая дополнительная аксиома, в частности, как утверждение, не требующее доказательства.
Лемма Цорна. Пусть 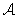 есть упорядоченное множество, в котором любое линейно упорядоченное множество имеет мажоранту. Тогда в
есть упорядоченное множество, в котором любое линейно упорядоченное множество имеет мажоранту. Тогда в 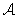 существует максимальный элемент.
существует максимальный элемент.
Множество 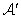 называется линейно упорядоченным, если для любых его элементов a и b выполнено или a < b, или a > b, или a = b . Элемент a называется мажорантой
называется линейно упорядоченным, если для любых его элементов a и b выполнено или a < b, или a > b, или a = b . Элемент a называется мажорантой 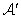 , если он не меньше любого элемента из этого множества (иное название для таких элементов - верхняя грань). Элемент a0 называется максимальным, если из неравенства
, если он не меньше любого элемента из этого множества (иное название для таких элементов - верхняя грань). Элемент a0 называется максимальным, если из неравенства 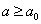 следует
следует 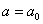 (не путать с наибольшим элементом, который определяется как элемент, больший всех остальных).
(не путать с наибольшим элементом, который определяется как элемент, больший всех остальных).
Одно из топологически эквивалентных представлений сферы с ручками
Линейная связность
Назовем топологическое пространство линейно связным, если для любых двух точек x0 и x1 существует непрерывная линия, их соединяющая, т.е. такое непрерывное отображение 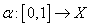 , что
, что 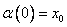 и
и 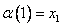 .
.
Эта хорошо известная фигура изображена на следующем рисунке.
Лузин Николай Николаевич (1883-1950)
Родился и окончил гимназию в г. Томске. В 1908 г. окончил Московский университет. С 1917 г. профессор этого университета. Н.Н. Лузин - один из создателей дескриптивной теории функций, создатель московской научной школы теории функций. Среди его учеников академики П.С. Александров, А.Н. Колмогоров, М.А. Лаврентьев.
Марков Андрей Андреевич (1903-1979)
Выдающийся математик. Занимался топологией, топологической алгеброй, динамическими системами, конструктивной математикой и логикой.
Непрерывность
Отображение называется непрерывным, если оно непрерывно в каждой точке.
Непрерывность в точке
Отображение 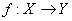 называется непрерывным в точке
называется непрерывным в точке 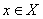 , если для любой окрестности Of(x) точки f(x) найдется окрестность Ox точки x такие, что
, если для любой окрестности Of(x) точки f(x) найдется окрестность Ox точки x такие, что 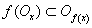
Несравнимые топологии
Топологии 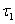 и
и 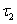 называются несравнимыми, если ни одно из включений
называются несравнимыми, если ни одно из включений 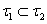 и
и 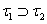 не имеет места, т.е. найдутся открытые множества открытые в первой топологии и не открытые во второй и наоборот.
не имеет места, т.е. найдутся открытые множества открытые в первой топологии и не открытые во второй и наоборот.
Нормальное пространство
Пространство называется нормальным пространством, если оно удовлетворяет аксиоме нормальности.
Односторонняя поверхность
Двумерное связное многообразие, которое нельзя раскрасить разными цветами
Окрестность
Окрестностью точки x в топологическом пространстве 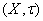 называется любое множество O , для которого существует открытое множество G такое, что
называется любое множество O , для которого существует открытое множество G такое, что 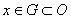 . Следовательно, открытые множества являются окресностями каждой своей точки. Окрестностью множества A в топологическом пространстве
. Следовательно, открытые множества являются окресностями каждой своей точки. Окрестностью множества A в топологическом пространстве 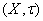 называется любое множество O , для которого существует открытое множество G такое, что
называется любое множество O , для которого существует открытое множество G такое, что 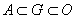 .
.
Операция переворачивания
Операция, при которой буквы в слове записываются в обратном порядке и в обратных степенях. Соответствует простому переворячиванию многоугольника на другую сторону.
Операция переименования
Это операция, при которой буква можно переименовывается в любую другую букву при условии, что она еще не была задействована.
Операция разрезания
Результат проведения дополнительного разрезания многоугольника на две части.
Операция склейки
Операция, обратная к операции разрезания.
Операция сокращения
Удаление из слов двух подряд идущих букв вида aa -1 или a -1a .
Открытое множество
Элементы топологии называются открытыми множествами.
Родился и вырос в Ленинграде, учился в знаменитой 239-й школе. В 1982 г. выиграл Международную математическую олимпиаду, набрав максимально возможное количество баллов. Степень кандидата наук получил в Петербургском университете, затем некоторое время работал в Петербургском отделении математического института РАН.
Пленка Мебиуса
То же самое, что и лист Мебиуса.
Топологическое пространство, в котором каждая точка 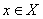 имеет окрестность Ox , гомеоморфную евклидову пространству
имеет окрестность Ox , гомеоморфную евклидову пространству 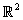 .
.
Подпространство
Пусть X есть топологическое пространство с топологией 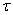 и
и 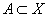 . Пространство
. Пространство 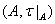 , где
, где 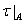 есть индуцированная топология, называется подпространством пространства
есть индуцированная топология, называется подпространством пространства 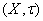 .
.
Покрытие
Семейство 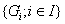 называется покрытием пространства X, если
называется покрытием пространства X, если 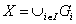 . При этом покрытие является открытым покрытием, если каждое множество Gi является открытым
. При этом покрытие является открытым покрытием, если каждое множество Gi является открытым
Предельная точка
Точка x называется предельной точкой множества A , если для любой ее проколотой окрестности, т.е. множества вида 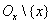 , где Ox есть окрестность точки x , выполнено
, где Ox есть окрестность точки x , выполнено 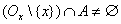 .
.
Проблема Пуанкаре
Всякое ли трехмерное компактное, связное многообразие без края, в котором каждая замкнутая кривая стягивается в точку, гомеоморфно трехмерной сфере S 3 ?
Производное множество
Множество всех предельных точек прикосновения называется производным множеством и обозначается через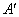 .
.
Проективная плоскость
Фактор-пространство, полученное из прямоугольника, и имеющее следующую развертку.
Другие определения проективной плоскости см. в параграфе с соответствующим названием.
Выдающийся французский математик, механик и философ. Считается одним из главных создателей новой науки, получившей впоследствии название топологии.
Равенство топологий
Две топологии равны, если они состоят из одних и тех же открытых множеств.
Развертка
Многоугольник, при некороторой склейке сторон которого получается данная поверхность.
Расширение
Топологическое пространство X называется расширением топологического пространства A, если A есть подпространство пространства X .
Регулярное пространство
Пространство называется регулярным пространством, если оно удовлетворяет аксиоме регулярности.
Ручка
Часть поверхности, гомеоморфная тору, на котором вырезана круглая дырка.
Свойство Суслина
Говорят, что топологическое пространство X имеет свойство Суслина, если любая система попарно непересекающихся открытых множеств в X не более чем счетна.
Связность, связное пространство
Топологическое пространство X называется связным, если его нельзя представить в виде объединения 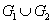 непустых открытых непересекающихся подмножеств
непустых открытых непересекающихся подмножеств 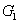 и
и 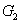 .
.
Связное множество
Подмножество топологического пространства называется связным множеством, если оно связно как подпространство с индуцированной топологией.
Сепарабельность
Пространство X называется сепарабельным, если оно имеет счетное, всюду плотное подпространство.
Сравнение топологий
Сравнить топологии − это указать, какая из следующих четырех ситуаций имеет место:
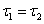 , т.е. имеет место равенстве топологий;
, т.е. имеет место равенстве топологий;
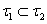 , топология
, топология 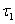 слабее топологии
слабее топологии 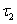 ;
;
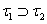 , топология
, топология 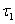 сильнее топологии
сильнее топологии 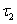 ;
;
топологии несравнимы, если ни одно из включений и не имеет места, т.е. найдутся открытые множества открытые в первой топологии и не открытые во второй и наоборот.
Стрелка Зоргенфрея
Так называется топологическое пространство, в котором на вещественной прямой 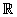 для любого
для любого 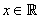 ф.с.о.
ф.с.о. 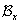 определяется состоящим из всех полуинтервалов
определяется состоящим из всех полуинтервалов 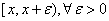 .
.
Стягивание в точку
Топологическое пространство называется стягиваемым в точку x0, если существует непрерывное отображение 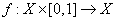 , где [0,1] - обычный отрезок с евклидовой топологией, такое, что для всех
, где [0,1] - обычный отрезок с евклидовой топологией, такое, что для всех 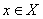 выполнено
выполнено 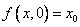 и
и 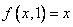 для всех.
для всех.
Суслин Михаил Яковлевич (1894-1919)
Ученик Н. Н. Лузина. С 1917 г. работал в Московском университете. Основным научным открытием М.Я. Суслина было установление факта существования А-множеств. М.Я. Суслин опубликовал только одну короткую заметку о своих открытиях (1917).
Сфера с ручками
Это сфера, в которой на месте некоторого конечного числа круглых дыр приклеены ручки.
Тихонов, Андрей Николаевич (1906-1993)
Окончил МГУ в 1927 г. С 1970 был деканом факультета вычислительной математики и кибернетики; заместителем директора института прикладной математики АН СССР. Первые работы посвящены топологии и функциональному анализу. А.Н. Тихоновым введено понятие произведения топологических пространств ("тихоновское произведение", 1926), доказаны теоремы о компактности произведения компактных пространств и о существовании неподвижной точки при непрерывных отображениях в топологических пространствах. Последующие труды относятся к теории дифференциальных уравнений, математической физике, геофизике и вычислительной математике.
Топологический инвариант
Топологическим инвариантом называется любое свойство, которое сохраняется гомеоморфизмами.
Топологическое пространство
Множество X, снабженное некоторой топологией 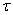 , т.е. пара
, т.е. пара 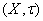 называется топологическим пространством. Элементы топологии, т.е. множества из
называется топологическим пространством. Элементы топологии, т.е. множества из 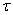 называются открытыми множествами.
называются открытыми множествами.
Топология
Пусть X -произвольное множество. Семейство 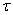 подмножеств множества X
называется топологией на множестве X , если выполнены следующие условия:
подмножеств множества X
называется топологией на множестве X , если выполнены следующие условия:
(O1) Объединение любого подсемейства семейства 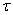 принадлежит
принадлежит 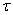 ;
;
(O2) Пересечение любого конечного подсемейства семейства 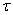 принадлежит
принадлежит 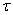 .
.
(O3) 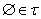 ,
, 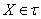 .
.
Топология сильнее
Топология 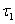 сильнее топологии
сильнее топологии 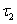 , если каждое открытое множество в топологии
, если каждое открытое множество в топологии 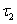 является открытым множеством в топологии
является открытым множеством в топологии 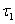 .
.
Топология слабее
Топология 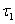 слабее топологии
слабее топологии 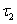 , если каждое открытое множество в топологии
, если каждое открытое множество в топологии 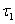 является открытым множеством в топологии
является открытым множеством в топологии 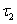 .
.
Точкой прикосновения
Точка 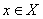 называется точкой прикосновения множества A, если любая ее окрестность Ox имеет непустое пересечение с множеством A.
называется точкой прикосновения множества A, если любая ее окрестность Ox имеет непустое пересечение с множеством A.
Тривиальная топология
Топология, состоящая всего из двух множеств: 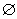 и X, называется тривиальной или антидискретной топологией.
и X, называется тривиальной или антидискретной топологией.
Урысoн Павел Самуилович (1898-1924)
Окончил Московский университет в 1919 г. П.С. Урысон - один из крупнейших специалистов в области топологии. Ему принадлежат также работы по нелинейным дифференциальным уравнениям, геометрии и др. Трагически погиб в Бретани (Франция) во время купания.
ф.с.о.
Сокращение от фундаментальной системой окрестностей.
Фактор-пространство
Пусть дано множество X и на нем задано отношение эквивалентности. Множество 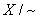 всех классов эквивалентности, наделенное фактор-топологией, называется фактор-пространством.
всех классов эквивалентности, наделенное фактор-топологией, называется фактор-пространством.
Фактор-топология
Сильнейшую среди всех топологий на множестве всех классов эквивалентности, для которых каноническое отображение, сопоставляющее каждой точке ее класс эквивалентности, является непрерывным.
Фрешe Морис Рене (1878-1973)
Французский математик. Профессор Страсбургского (1919-1927) и Парижского (1928-1949) университетов. Основные работы Фреше относятся к топологии и функциональному анализу, где он ввел современные абстрактные понятия метрического пространства, компактности, полноты и др. Работал также в области теории вероятностей.
Фундаментальной системой окрестностей
Фундаментальной системой окрестностей (сокращенно ф.с.о.) точки x в топологическом пространстве 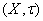 называется такое семейство
называется такое семейство 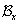 окрестностей этой точки, что для каждой окрестности O точки x существует
окрестностей этой точки, что для каждой окрестности O точки x существует 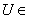
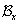 , удовлетворяющее условиям
, удовлетворяющее условиям 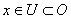 .
.
Хаусдорф Феликс (1868-1942)
Немецкий математик. В 1891 г. окончил Лейпцигский университет. Основные его труды относятся к теории множеств, топологии, функциональному анализу. В 1942 г., узнав о предстоящей отправке семьи в гитлеровский концлагерь, покончил жизнь самоубийством.