4.8. Поверхности и их развертки

Задача 18. Какая поверхность закодирована словом ?

Решение.  Многоугольник, закодированный словом , выглядит следующим образом:

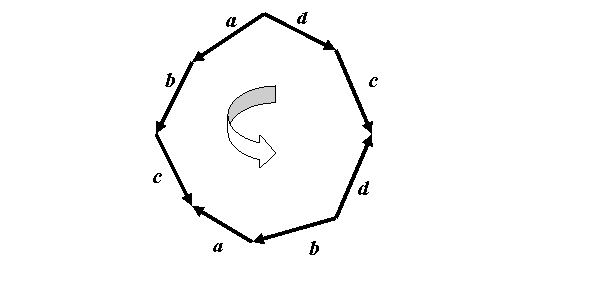
Мы просто движемся по кругу против часовой стрелки (такое направление в математике чаще всего принимают за положительное). Первая степень соответствует стрелке, идущей по ходу движения, а степень -1 соответствует стрелке с направлением против хода движения.

Т.к. в нашем слове каждая буква встречается в противоположных степенях, то наша поверхность является двухсторонней.

Мы знаем, что в таких словах обязательно должны встречаться четверки из двух букв, которые чередуются. Например, это следующие четверки:  abca^-1b^-1dc^-1d^-1,  abca^-1b^-1dc^-1d^-1, abca^-1b^-1dc^-1d^-1. Выберем для определенности первый вариант, т.е. пусть выделенными будут буквы a и c.

Cм. файл

Задача 19. Какая поверхность закодирована словом ?

Решение.

См. файлы файл 1 и файл 2

Предыдущие две задачи можно решить чисто формальным способом, если мы воспользуемся  двумя формулами, доказанными в замечаниях 35 и 38. Это формулы  

 и . Напомним, что заглавными буквами в них обозначены некоторые и в принципе произвольные наборы букв.

Задача 20. Найти формальное решение задач 18 и 19.

Решение задачи 20.

А)Случай задачи 18. Заданное слово имеет вид . Мы выделяли буквы  и , пусть оно будет цветным:

abca^-1b^-1dc^-1d^-1. Чтобы не было недоразумений с  буквами нашего конкретного примера, мы перепишем первое наше тождество в виде: . В нашем конкретном случае заглавные буквы имеют следующий смысл:  и . Тогда получим abca^-1b^-1dc^-1d^-1~ aca^-1c^-1bd^-1b^-1d. Т.е. получили каноническое слово для поверхности сферы с двумя приклеенными двумя ручками.

Б) Случай задачи 19. Наше слово имеет вид . Выделим две буквы в одинаковых степенях. Пусть это будет буква а и применим формулу: . Тогда  и  и поэтому .

Далее выделяем букву b . Предварительно циклической перестановкой букв:   выведем выделенную букву на первое место. Опять используем формулу , только теперь мы в ней заменим букву  на . Здесь у нас уже  и . Мы получим  .

В третий раз используем ту же формулу  , в которой мы предусмотрительно заменили имя интересующей нас буквы на с. Имеем: ~ (циклическая перестановка),  и . Тогда ~. Таким образом, мы получили слово из трех двоек вида , т.е. наша поверхность является сферой, к которой три круглых дырки заклеены тремя листами Мебиуса.

Замечание. Таким образом, мы видим, что задачи 18 и 19 можно решить чисто формально, не обращаясь к манипуляциям с многоугольниками. Советуем, однако, не увлекаться последним способом, а затратить время на две-три задачи с тем, чтобы досконально понять, что же происходит при наших манипуляциях со словами.

Задача 21. Разверткой какой поверхности без края (при условии приклеивания необходимого количества круглых дисков) являются следующие две фигуры:

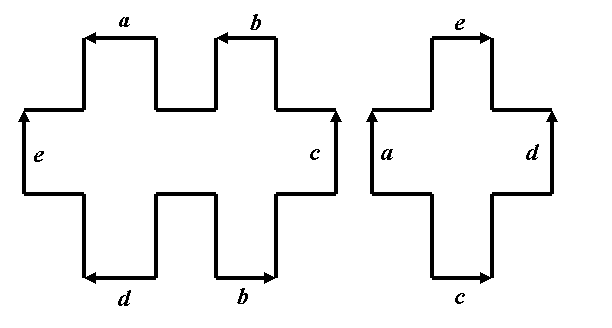
Начало решения и конец решения

Итак, мы пришли к слову . Далее мы используем формальный метод решения, рассмотренный нами в задаче 20. Выделим цветом букву, которая является ведущей в наших преобразованиях: 44~44. Череда последующих сокращений приводит нас к слову 44. Таким образом, наша поверхность является проективной плоскостью.

Задача 22. Какой поверхности соответствует слово ?

Решение. Поскольку каждая буква присутствует в данном слове обязательно в разных степенях, то наша поверхность является двухсторонней. Далее будем использовать метод математической индукции.

При  мы имеем слово , соответствующее сфере с одной ручкой, т.е. тору. Выскажем предположение, что для произвольного натурального числа  мы имеем сферу с  ручками и пусть оно верно для заданного .  Возьмем следующий номер.  Тогда слово примет вид:

В качестве ведущей четверки выберем буквы в этом слове с номерами  и . Тогда это слово можно записать в виде

, где  и .

Далее нам нужна формула, которую мы уже выше неоднократно использовали:

. В нашем случае слова  и  следует считать пустыми, т.е. не содержащими букв. Получаем слово

.

Первая четверка нам дает одну ручку, приклеенную к остальной части поверхности, а она, т.е. поверхность с разверткой  фактически совпадает с поверхностью, закодированной первоначально заданным словом. Нужно только переименовать в этом слове каждую букву  на  и наоборот. Но по предположению индукции эта часть нам дает еще  ручек. Индукция полная и это завершает доказательство.