4.6. Сепарабельность. Первая и вторая аксиомы счетности. Условие Суслина

Задача 11. На плоскости  топология задана следующим выбором окрестностей: если , то ф.с.о. точки  составляют множества

и множества

в случае . Сепарабельны ли следующие подпространства:

          D - ось абцисс?

Решение. Если точка  находится строго выше оси абцисс, то ее окрестность есть объединение интервала и прямоугольника в нижней части плоскости. Это множество изображено синим цветом на следующем чертеже.

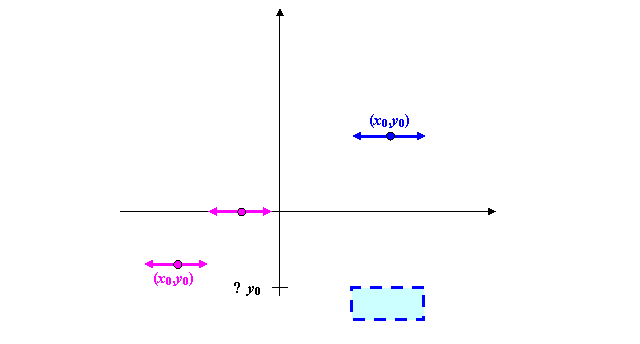
Розовым цветом изображена окрестность для точек в нижней полуплоскости. Также в виде горизонтального интервала должны быть изображены окрестности точек на оси абцисс.

Начнем обсуждение задачи со второго множества В. Это подмножество в индуцированной топологии в качестве окрестностей будет иметь только горизонтальные интервалы (нижние прямоугольники «обрежутся». Заметим далее, что это подпространство не имеет свойства Суслина: семейство всех горизонтальных прямых в верхней полуплоскости суть несчетное семейство открытых попарно не пересекающихся множеств. А если пространство не имеет свойства Суслина, то оно и не является сепарабельным.

По той же причине не является сепарабельным множество С.

Множество D  является сепарабельным, ибо в индуцированной топологии оно по сути совпадает с евклидовой прямой и множество всех рациональных точек является сепарабельным.

Множество А не является сепарабельным, т.к. пересечение точки  могут лежать только на тех горизонтальных прямых, на которых уже лежат точки множества А. Следовательно, эти точки могут уместиться только на счетном числе горизонтальных прямых и, следовательно, не заполняют плоскость.

Задача 12. Окрестностью точки  на прямой  объявляется произвольное множество вида

где  и последовательность чисел  выбрана произвольно. Будет ли это пространство удовлетворять 1-ой аксиоме счетности?

Решение.  Окрестность точки  состоит из самой точки и последовательности произвольно уменьшающихся интервалов, «стремящихся» к самой точке .

Длины интервалов образуют произвольно заданную последовательность  чисел . Докажем, что данное пространство не удовлетворяет первой аксиоме счетности. Для этого мы будем использовать «диагональный» метод Кантора. Предположим, от противного, что точка  имеет счетную ф.с.о. , где каждое множество  имеет указанный выше вид. Следовательно, каждому множеству  соответствует некоторая последовательность . В результате мы получаем следующую таблицу:

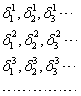
Выберем теперь последовательность строго положительных чисел  так, чтобы  для всех . Пусть, далее, окрестность  задана формулой:

Заметим, что значение числа  особого значения не имеет и мы взяли его равным 1. Нетрудно теперь понять, что множество  не может содержать никакого множества  ни для какого натурального числа . И причина здесь очень проста - она в неравенстве . Полученное противоречие доказывает утверждение.

Задача 13. Для каждой точки  плоскости  определим ф.с.о. как совокупность всех множеств вида , . Будет ли это пространство

1) сепарабельно?

2) иметь первую аксиому счетности?

3) удовлетворять условию Суслина?

4) иметь счетную базу?

Решение. Окрестностями точек мы объявили хорошо известные «брусы», у которых левая нижняя угловая точка есть именно заданная точка.

1) Заданное пространство является сепарабельным. В самом деле, хорошо известно свойство рациональных чисел: в любом интервале  есть рациональные числа. Этот факт проистекает из способа построения вещественной прямой из множества рациональных чисел как дедекиндовых сечений (а в средней школе используются бесконечные десятичные дроби). Отсюда можно вывести, что в любом брусе есть точка  с обеими рациональными координатами.  Следовательно, квадрат  множества рациональных чисел является счетным и всюду плотным.

2) Пространство имеет первую аксиому счетности. В качестве счетной фундаментальной системы окрестностей точки  можно взять систему брусов , где .

3) Сепарабельное пространство имеет свойство Суслина, поэтому положительный ответ следует из пункта 1).

4) Известна и почти очевидна теорема, что подпространство пространства со счетной базой само имеет счетную базу. Рассмотрим на плоскости диагональ . Легко понять, что это подпространство является несчетным дискретным пространством. Любая база в дискретном пространстве должна содержать все одноточечные множества (кстати, ответьте: почему?) и потому несчетна.