2.4.5. Метод чисел Фибоначчи

Рассмотрим еще один оптимальный метод последовательного поиска минимума. Идея этого метода состоит в выборе такой последовательности , для которой уменьшение длины интервала неопределенности было бы максимальным из возможных значений. Такая задача была поставлена и решена Дж. Кифером в 1953 году, причем ее решение оказалась связано с работами математика XII века Леонардо Пизанского (Фибоначчи) и его знаменитыми числами.

Подобно методу золотого сечения процедура метода чисел Фибоначчи требует два вычисления значения функции на первой итерации, а на каждой последующей – только по одному. Однако эта процедура отличается от метода золотого сечения тем, что величина сокращения интервала неопределенности меняется от итерации к итерации и число итераций задается до решения задачи.

Зададим - число итераций и вычислим  первых чисел последовательности Фибоначчи:

(2.8)

В таблице 2.5 приведены первые 20 чисел этой последовательности.

Таблица 2.5

1 2 3 4 5 1 2 3 5 8 6 7 8 9 10 13 21 34 55 89 11 12 13 14 15 144 233 377 610 987 16 17 18 19 20 1597 2584 4181 6765 10946

Предположим, что на -ой итерации интервал неопределенности равен . Рассмотрим две точки  и , определяемые следующим образом:

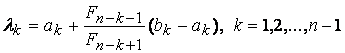,	(2.9)
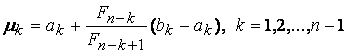,	(2.10)

здесь n - заданное общее число вычислений функции.