2.4.6. Сравнение методов линейного поиска

Сравним рассмотренные выше методы линейного поиска. При заданной на интервале  строго квазивыпуклой функции  каждый из рассмотренных методов дает за конечное число шагов такую точку , что , где - длина конечного интервала неопределенности, а - точка минимума на заданном интервале. Для фиксированного значения  наименьшее число требуемых вычислений функции отвечает более эффективному алгоритму.

 Число вычисления функции  можно определить из неравенств []:

Базара М., Шетти К. Нелинейное программирование. Теория и алгоритмы.- М.: Мир, 1992. - 584с. Полный список литературы

• при дихотомическом поиске ,
• при использовании метода золотого сечения ,
• в случае метода чисел Фибоначчи .

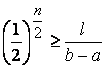В таблице 2.6 приведено сравнение коэффициентов уменьшения интервалов, полученных различными методами, для различных значений числа  [].

Мину М. Математическое программирование. - М.: Наука, 1990. - 488с. Полный список литературы

Таблица 2.6

	Дихотомический поиск	Золотое сечение	Метод чисел Фибоначчи
10-2 10-3 10-3 10-5 10-6	17 23 29 35 42	13 18 22 27 31	11 15 20 25 30

Сравним метод золотого сечения с методом чисел Фибоначчи.

Известно, что члены ряда Фибоначчи удовлетворяют формуле Бинэ []:

Воробьев Н. Н. Числа Фибоначчи. - М.;Наука,1969.-112с. Полный список литературы

,

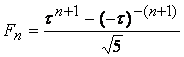где .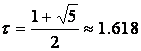

При больших значениях  можно приближенно положить

.

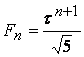Тогда

,

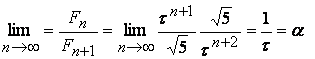где .

Например,

.

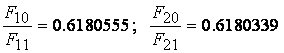Таким образом, для достаточно больших - числа вычислений функции  оба метода приводят к одному и тому же расположению точек и .